전기기능사 필기 대비 정전력과 전계의 세기를 공부한다. 전계는 전기장이라고도 하고 전장이라고도 한다. 한 가지로 통일하면 안 되나. 정전력을 말하는 쿨롱의 법칙은 차라리 쉽다. 전계의 세기, 전속의 밀도로 들어가니 더 복잡하고 개념을 잡기도 어렵다. 갑자기 처음 보는 공식을 대입하여 해결하는 저자의 설명은 무성의하다.
쿨롱의 법칙도 수박 겉핥기 방식으로 넘어가니 외워지지가 않는다. 한 페이지에 외계어 같은 공식이 2~3개는 나오는 것 같다. 다 외워야 하나 싶지만 문제 풀이를 하면서 외워지기도 한다.
1. 정전력과 쿨롱의 법칙
정전력(서로 반발과 흡인의 힘, F)의 크기는 쿨롱의 법칙을 따른다. 두 점 전하 사이에 발생하는 정전력의 크기는 두 전하(전기) 량의 곱에 비례하고 두 전하 사이의 거리의 제곱에 반비례한다. 글로 쓰여있는 쿨롱의 법칙을 이해하기란 쉽지 않다. 문제풀이를 통하여 이해하는 것이 빠르다.

쿨롱의 법칙 공식(정전력의 크기)
두 점전하 사이에 작용하는 정전력의 힘, 크기(Force, N)는
두 전하(전기량)의 곱에 비례하고
전하 사이의 거리의 제곱에 반비례한다.
그리고 진공 중의 점(구체) 전하의 유전율과 유전체의 비유전율이 상수로 들어간다.

진공유전율(Eo)은 8.855 x 10^-12 [F/m]이니 이를 수치로 환산하면,
진공 중의 점전하의 유전율은
1 / 4πEo
= 1/ 4π x 8.855 x 10^-12
= 9 x 10^9 이 나온다. 최종 정전력 공식은 아래와 같이 볼 수 있다.
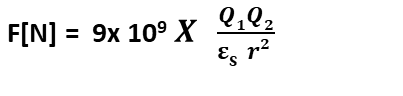
F(Force) =정전력의 크기, 단위는 N(Newton)
Eo = 진공 중의 유전율, 8.855 x 10m^-12 [F/m]
Es = 임의의 유전체의 유전율
r = 두 전하 사이의 거리
Q1, Q2 = 두 점의 전하량
문제)
같은 양의 점전하, 진공 중 0.5m 간격, 이때 작용하는 힘이 0.1N이다. 점전하의 전기량[uC]?
간격이 있다는 것은 두 개의 점전하의 정전력을 구하는 것인데 단위가 [uC]이다. 쿨롱의 법칙을 적용하여
F(N) = 1/4πEo X (Q1xQ2) / Es.r^2
F = 0.1 [N]
1/4πEo = 9X10^9
Es = 1 (진공 중이라 했으니 비유전율)
0.1 = 9 x 10^9 x (Q1 Q2) /1 x 0.5^2
Q1, Q2 가 같은 값이니 Q^2으로 보고
Q^2 = 0.1 x 0.5^2 / 9 X 10^9
= 2.777 x 10^-12, 제곱근을 구하면,
Q = 1.66666 x 10^-6 [C]
= 1.66 [uC]
** 제곱을 잊으면 안 된다.
** 공식을 알고 단위만 헷갈리지 않으면 문제가 없어 보인다.
단위 전하
진공 중에서 동일한 전하를 1m 거리에 놓았을 때 작용하는 힘의 크기(정전력)가 9 x 10^9 이 되었을 때 이때 전하의 크기를 1 [C]이라 한다.
** 진공 중 점전하의 유전율인가?
** 잘 이해가 안 되지만 차차 이해할 수 있으리라 생각한다.
2. 전기장(전장, 전계)의 세기와 방향
전계의 세기(E, V/m)
- 전계의 세기는 전계 내의 임의의 한 점에 단위전하 + 1(C)을 놓았을 때, 이에 작용하는 힘
** "전계의 세기"는 "전장의 세기"라고 시험문제에 나오기도 한다.
- 전계의 세기는 임의의 한 점에서의 전기력선 밀도와 같다.
- 전계의 세기는 거리의 제곱에 반비례하여 증감한다.
- 단위는 전압/거리(V/m)
한 개의 점전하에 의한 전계의 세기
전계의 세기를 구하기 위해서는 Q [C]의 전하로부터 1m 떨어진 지점에 1 [C]의 전하를 놓았을 때 이 1 [c]의 전하에 작용하는 힘(Force, N)을 구한다.
** 다른 말로는 진공 중에 동일한 전하를 1m 거리에 놓았을 때 작용하는 힘이 9x 10^9이 될 때 전하의 크기가 1 [C]이 된다. 같은 말 같다.
전계의 방향은 전하의 부호까지 포함하여야 한다.
그 전계의 세기는 전하량에 비례하고 거리의 제곱에 반비례하여 증감한다.
전계의 세기공식,
정전력의 크기를 구하는 쿨롱의 법칙 공식에서 두 지점이 아닌 한 지점만을 표시한 것과 같다.

정전력과 전계의 세기의 관계
정전력은 Q1 X Q2, 전계의 세기는 Q 1개만 들어간다. 그래서 전계의 세기(E)에서 Q(전하량)를 곱하면 정전력의 세기(F)가 된다.
F = E x Q [N] 이 된다.
정전력(F)의 단위는 [N]
전계의 세기(E)의 단위는 [V/m]
문제)
전장의 세기가 100 [Vm], 의 전장에 5 [uC]의 전하량을 놓으면 작용하는 힘은?
"전장의 세기"가 주어졌다.
5 [uC] = 5 x 10^-6 [C]
F = E.Q의 공식을 적용한다.
F = 100 x (5 x 10^-6)
F = 5 x 10^-4
정전력과 전계의 세기의 관계
MKS 단위계에서 전계의 세기(E)는 Q = 1 [C, 쿨롱]에 작용하는 힘이 1 [N, 뉴튼]이 되는 것으로 전계의 세기의 단위는 다음과 같다.
E = N/C

J / C = V, (V = (일한 양 W [J]) / (전하량 Q [C]) 이기에 전계의 세기는 E = [V / m]의 단위를 유도할 수 있다.
** 여러 공식을 더 배워야 할 것 같다.
3. 전계의 계산
전계의 세기 E는 r 점에 있어서의 전계의 세기이다. 전계의 구성형태에 따라 전계의 세기가 다르다.
① 균일하게 대전된 구체의 r 점에서 전계의 세기
- 점전하의 전계의 세기와 같다.
- 4πr ^2은 구체의 표면적과 같은 거리이다.

문제)
증류수 중에 놓인 반지름 r의 도체구에 Q의 전하를 주었을 때 표면 전장의 세기는?
구체는 점전하의 전계(전장)의 세기와 같다.
1 / 4ㅠEo r^2 x Q / Es r^2 [N]
Q / 4ㅠEo Es r^2
증류유수의 비유전율, Es = 100
Q / 4ㅠEo r^2 x 100
* 유전체가 진공 중이면 Es = 1이 된다.
② 균일하게 대전된 무한히 긴 원통의 r 점에서 전계의 세기
- 2πr 은 원통의 원둘레와 같은 거리이다.
- 여기서 전하량(Q)은 원통 길이 1m 당 전하량[C/m]

③ 균일하게 대전한 무한 넓은 평면에 의한 전계
- 무한히 넓어 면적을 알 수 없으니 1평방미터 당 전하량 [C/1㎡]을 쓴다.
- σ = 1평방미터 당 전하량 [C/1㎡]

④ 균일하게 대전한 무한 넓은 평행판에 의한 전계
- 무한히 넓어 면적을 알 수 없으니 1평방미터 당 전하량 [C/1㎡]을 쓴다.
- σ = 1평방미터 당 전하량 [C/1㎡]

** 근데 2라는 수치는 왜 빠졌을까?
⑤ 대전한 도체 표면의 전계
- 위의 무한히 넓은 평행판에서의 전계와 같다.

** 내겐 무척이나 어렵다.
■■
'전기기능사 도전' 카테고리의 다른 글
| 전기기능사 필기 - 자석과 쿨롱의 법칙 (0) | 2023.01.14 |
|---|---|
| 전기기능사 자격증 필기대비- 정전용량(콘덴서) (1) | 2023.01.14 |
| 전기기능사 필기 대비 - 전속과 전위 (0) | 2023.01.13 |
| 전기기능사 도전 - 정전 에너지 (1) | 2023.01.11 |
| 전기기능사 필기- 유전율과 비유전율 이해 (0) | 2023.01.10 |
| 전기기능사 필기 도전 - 정전기 (0) | 2023.01.06 |
| 전기기능사 도전, 전기 단어와 개념들 (0) | 2023.01.03 |




댓글