기전력(전자의 이동)을 발생시키는 요인으로는 자기장 내의 자속의 변화를 일으키거나 코일에 전류의 변화를 일으키게 하는 것이다. 즉, 자속으로 인하여 자장과 전자이동이 생기고 전류를 넣으면 자장이 생기고 다시 전자의 이동이 생긴다. 전자유도이다.
1. 자속에 의한 기전력
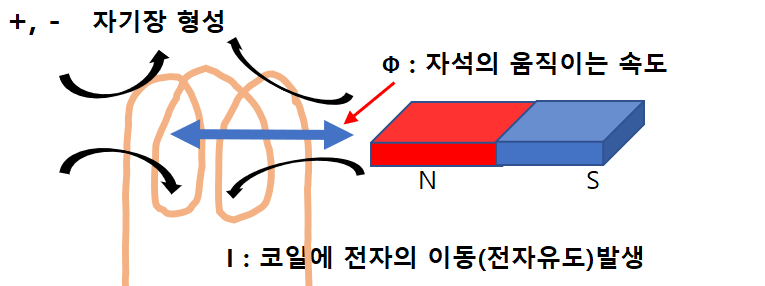
코일에 자석을 넣었다 뺏다 하면 자기장이 생긴다. 이때 렌츠의 법칙에 따라 자기장은 자속의 변화를 방해하는 방향으로 전류(기전력의 방향)가 발생한다.
이때 기전력은
코일의 감은 횟수와
자석의 속도(Δ Ф)와 시간의 변화(Δ t)에 따라(패러데이 법칙) 변한다.
** 시간이 분모라서 짧은 시간에 빨리 움직여야 기전력이 커진다.
그래서
기전력의 크기 e = 코일의 권수, 자속에 비례하고 시간에 반비례한다. 당연히 자속의 변화를 방해하는 방향으로 전류가 생기기에 아래의 공식처럼 " - " 로 표시한다.

여기서
Δ Ф = 자속의 속도의 변화
Δ t = 시간의 변화, "Δ"는 변화값을 하니 빼면,
e = NФ / t [Wb],
= NФb NФb는 쇄교 속수라고 한다.
** "쇄교속수", 너무 어려운 말을 쓰는데 다행히도 시험문제에는 안 나오는 듯하다.
2. 직선운동에 의한 유도 기전력
도체의 길이와 자속밀도와 속도의 곱에 비례한다. 이때 기전력의 방향은 프레밍의 오른손 법칙에 따라 중지 방향으로 결정된다. e = Bℓv [V] , 여기서 도체의 이동이 발생하고 도체의 이동이 자속을 끊는 속도(v)의 방향 값인 sinθ 가 추가된다.
e = B ℓ v sinθ [V]
e : 유도기전력
B : 자속밀도
ℓ: 도체의 길이
v : 도체의 운동 속도
sinθ : 도체의 이동 각도
문제를 풀어보며 이해해야겠다.
문제)
길이 10cm 도선이 자속밀도 1 [wb/m2]의 자장 속에 자장과 수직방향으로 3초 간 15m 이동했다면 유기되는 기전력의 크기[V]는?
밀도 B, 길이 l, 이동 속도(거리/시간) 등등이 나오 도선이니 직선의 기전력의 공식을 사용한다.
e = B ℓ v sinθ [V]
길이 10cm = 0.1m다.
수직이니 sin90 = 1
속도 = 거리 / 시간 = 15/3 = 5
= 1 x 0.1 x 5 x 1
= 0.5 [V]
** 이 정도의 문제라면 단위에 주의하고 공식만 알면 쉬운 문제에 속한다.
3. 전류에 의한 기전력
- 인덕턴스(inductance) L [H, Henry]
전류의 변화에 의해 발생되는 기전력을 발생시키는 도체의 (전자유도) 능력을 인덕턴스라고 한다. 기전력을 일으키는 것을 인덕터라고 한다(코일 같은 것). 기전력은 자속의 시간적 변화나 전류의 시간적 변화에 의해 발생한다.
기전력 e = (전류의 변화 / 시간의 변화) x 인덕턴스

L = 인덕턴스
Δ I = 전류의 변화
Δ t = 시간의 변화,
여기서 L을 도체(코일)의 자체인덕턴스라고 한다
L 값은 코일의 권수, 철심의 형상, 재질에 의해 결정된다.
문제를 풀어보며 이해해야겠다.
문제)
80 mH의 코일에 흐르는 전류가 0.2초 동안 20A가 변했다. 이때의 기전력 [V]은?
80 mH라는 말은 인덕턴스(L) 값이다.
전류가 만드는 기전력 공식은
e = 인덕턴스 x 전류변화량 / 시간변화
8mH = 80 x 10^-3H이다.
e = L x dI / dt [V]
= (80 x 10^-3) x 20A / 0.2초
= (80 x 10^-3 ) x 100
= 8000 x 10^-3
= 8
** 단위에 주의하고 공식만 알면 쉽다.
인덕턴스 값의 유도
자속의 변화에 의한 기전력과 전류에 의한 기전력을 비교하여, Δ t를 동시에 지우면 여기서 인덕턴스(L)를 유도할 수 있다. 인덕턴스는 코일에 감은 권수와 자속에 비례하고 전류에 반비례한다. (전류가 크면 인덕턴스가 작아지나? 많은 전류가 필요 없나?)


L = 인덕턴스
N = 권수
Ф = 자속
I = 전류
** 인덕턴스 공식 안에 코일의 권수가 포함되어 있는 것은 알겠는데. 자속은 왜 들어가는지 모르겠다 공부가 더 필요하다.
4. 자기 유도와 상호유도
자기 유도
전류의 변화에 의한 쇄교자속의 변화로 코일 자체의 유도작용이 발생하여 역기전력이 유도된다. 한 개의 코일 안에서 전류가 흐르고 기전력이 발생하고, 다시 전류를 유도하고 이런 것 같다.
상호유도
코일이 두 개가 서로 근접하면 한쪽에만 전류를 흘려도 다른 쪽 코일에도 기전력이 발생한다는 것으로 보면 될 것 같다.
기전력은 자속 방해 방향 렌츠 - "렌츠를 들고 방해 마!"
기전력은 속도와 시간 패러데이 - "빨리데이"
기전력의 방향은 - "플레밍의 오른손 중지"
** 전자유도에서 생기는 유기기전력의 방향 - 렌츠 법칙
** 발전기의 유기 기전력의 방향을 알기 위한 법칙 - 플레밍의 오른손 법칙
** 전동기의 회전 원리는 플레밍의 왼손 법칙
** 이 차이가 무엇인지 아직 이해가 안 된다.
■■
'전기기능사 도전' 카테고리의 다른 글
| 전류에 의한 자기장과 자기장(자계)의 세기 (0) | 2023.01.15 |
|---|---|
| 전기기능사 필기 - 자석과 쿨롱의 법칙 (0) | 2023.01.14 |
| 전기기능사 자격증 필기대비- 정전용량(콘덴서) (1) | 2023.01.14 |
| 전기기능사 필기 대비 - 전속과 전위 (0) | 2023.01.13 |
| 전기기능사 도전 - 정전 에너지 (1) | 2023.01.11 |
| 전기기능사 필기- 정전력과 전계의 세기 (0) | 2023.01.10 |
| 전기기능사 필기- 유전율과 비유전율 이해 (0) | 2023.01.10 |




댓글